在ChatGPT成为万众瞩目的焦点之际，另一个AI应用也掀起了一小股热潮，那就是MidJourney。MidJourney是一个AI绘画应用，用户通过输入文字描述即可获得相应的图像。最新发布的Midjouney v5 进一步提高了图像生成质量，还解决了一直被诟病的手部细节问题，使人不得不感叹于人工智能的进步速度。除了MidJourney，DALL-E 2和Stable Diffusion也是为人所熟知的图像生成模型。而这三者背后采用的技术则都是以扩散模型（Diffusion Models）为基础的。

自2020年 DDPM（Denoising diffusion probabilistic models [1]） 发表以来，大量关于Diffusion Models 的论文如雨后春笋般层出不穷。仅CVPR 2023 就有100多篇的相关工作，其在学术界的热度可见一斑。Diffusion Models的原理看似简单，但其涉及的数学推导也着实令人头大。这篇文章将基于DDPM详细介绍扩散模型的原理，并给出笔者的一些理解。实际上，这篇文章是一份笔记，它主要参考了“Understanding Diffusion Models: A Unified Perspective”这篇论文。

目录

1. What are Diffusion Models?
   1. Diffusion Process
   2. Denoising Process
2. Hierarchical Variational Autoencoders
   1. Evidence Lower Bound (ELBO)
   2. Variational Autoencoders
   3. Hierarchical VAE
3. Variational Diffusion Models
4. Reference

What are Diffusion Models?

首先，简单介绍一个常见的图像生成任务。给模型一组观测到的图像数据 ，如一组人脸图像或者动物图像，其中 表示一张图像， 是图像数据的总量，我们希望模型从数据中学习到信息后能够生成一组和数据集尽可能相近的图像。这个过程的本质是建模数据集的真实分布，如果我们能够获悉数据集的真实分布，就可以从中采样得到符合分布的图像数据。而扩散模型就是建模上述过程的一种方法。

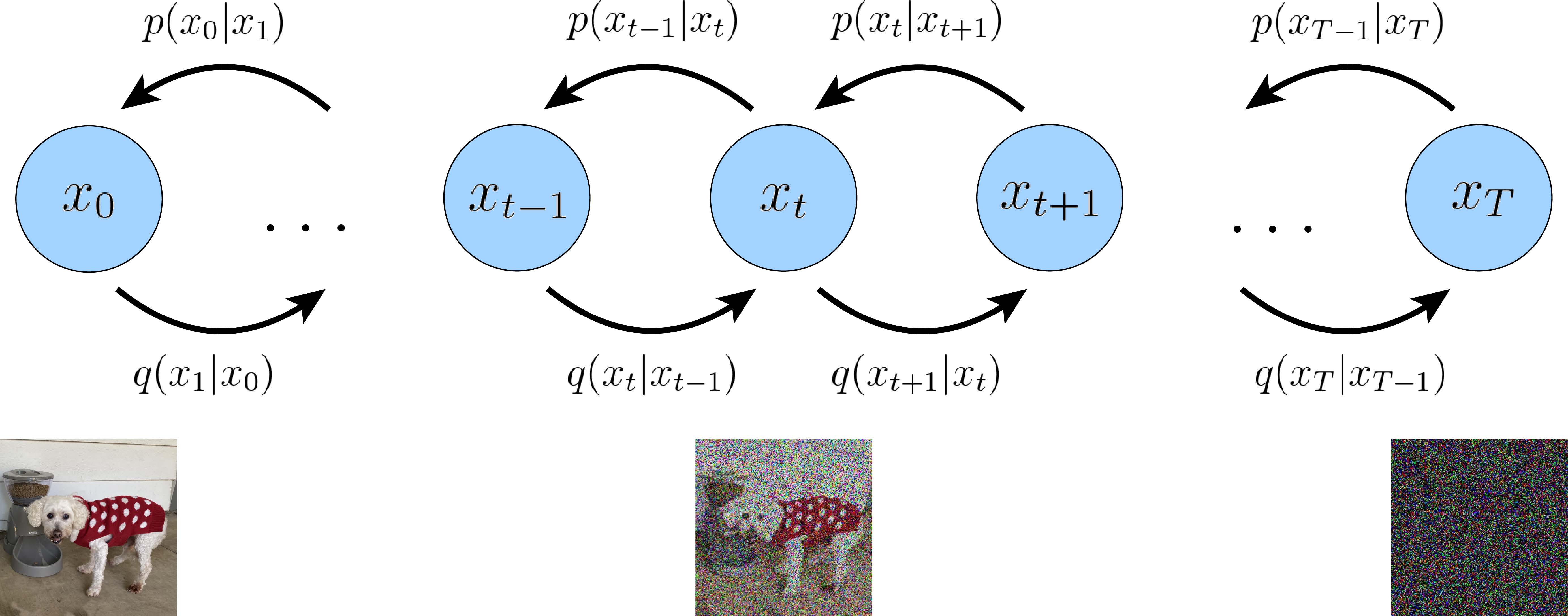
The illustration of diffusion models

简单来说，扩散模型包含两个过程：前向扩散过程和反向去噪过程。前向扩散过程是对一张图像逐渐添加高斯噪声直至变成随机噪声，而反向生成过程是去噪过程，我们将从一个随机噪声开始逐渐去噪直至生成一张合理的图像。

Diffusion Process

前向扩散过程对一张图像逐渐添加高斯噪声直至变成随机噪声，它可以看作一个固定的马尔可夫链（Markov chain）。给定原始数据 , 扩散过程通过 步扩散将原始图像转换为随机噪声，每一步都以上一步得到的数据为中心进行高斯采样：

其中参数 是可学习的或者是预置的超参数。扩散过程有一个特性，即我们可以从 直接获得任意时间步 对应的扩散版本 。

其中， 。当 是预置的超参数时，前向过程中则不包含可学习的参数，也就是说前向过程不需要优化。

公式(2)的证明如下：

推导过程利用了两个独立高斯随机变量之和仍然是高斯分布的事实。新分布的均值是两个均值的总和，方差也是两个方差的总和。Sum of two independent Gaussian random variables

Denoising Process

扩散过程是将数据噪声化，那么反向过程就是一个去噪的过程。如果我们知道反向过程中每一步的真实分布 ，那么从一个随机噪声 开始，逐渐去噪就能生成一个真实的样本，所以反向过程也就是生成数据的过程。

然而，真实分布 是不可知的，因此我们尝试用一个神经网络来建模一个分布 来近似真实分布。这样，最终生成的图像就可以表示为：

接下来的问题就是如何对 进行建模了。尽管 是不可知的，但是我们却可以导出 :

从中可以看出，反向去噪也是一个逐步高斯采样的过程，不过它并不是马尔可夫链。因为 不仅依赖于 ， 还依赖于。另外，我们可以观察到，公式(4)中的高斯分布的方差是确定的（ 是预置的常量）。

因此，我们也可以用类似的形式建模 ：

在反向生成过程中， 是已知的，我们只需要让神经网络建模 即可，即 。也就是说我们希望训练一个模型能够在给定任意时间步的输入 时估计出原始的图像数据 。

上面介绍了扩散模型的前向扩散过程和反向去噪过程。然而，我们对于为何要如此建模以及如何优化尚且不明。接下来，我们将从分层变分自编码器（Hierarchical Variational Autoencoders）的角度切入。

Hierarchical Variational Autoencoders

让我们回到最初的问题。给模型一组观测到的图像数据，我们希望模型能够建模数据的真实分布，从而可以生成一组和数据尽可能相近的图像。由于真实数据的维度较高，存在着一些隐含的因素和规律，这些因素往往难以直接观察和描述，导致了建模的困难。通常，我们可以认为观察到的数据是由一个相关的看不见的隐变量 表示或生成的。因此，可以尝试从隐变量的角度潜在地揭示观察到的数据的语义结构。

形式上，我们将隐变量 与观察到的数据 表示为一个联合概率分布 。基于极大似然的思想，我们期望获得一个生成模型可以最大化在所有观察数据 上的似然函数 。根据边缘概率分布，我们可以得到

或者，根据概率的链式法则：

不论何种形式，我们都无法直接计算 。公式(9)需要对 积分，公式(10)则需要获取隐变量的后验概率。

不过，我们可以通过优化一个代理目标函数来最大化似然函数，即证据下界（Evidence Lower Bound, dubbed ELBO）。

Evidence Lower Bound (ELBO)

形式上，ELBO可以表达为：

其中， 是一个参数化的隐变量编码器。ELBO的导出过程如下：

由于KL散度总是大于等于0的，所以ELBO是 的下界。通过最大化ELBO就可以间接最大化 。而且，二者之间的差是近似后验概率 与真实后验概率 之间的KL散度。本质上，最大化ELBO项就是最小化KL散度项。

我们引入隐变量 之后，我们的目标是学习这个描述我们观察到的数据的隐式结构。换句话说，我们要优化我们的变分后验 的参数，使之与真实的后验分布 完全匹配，也就是最小化它们的KL散度。

因此，我们通过最大化ELBO实现了曲线救国。这一定程度上是无奈之举，因为直接优化KL散度行不通（真实后验分布 是不可知的）。

Variational Autoencoders

变分自编码器（Variational Autoencoders）就是通过直接最大化ELBO做生成任务的。其优化目标可以表示为：

在这种情况下，我们同时学习了一个编码器（Encoder）和一个解码器（Decoder）。编码器将输入数据 映射到一个瓶颈分布 得到对应的隐变量 ；解码器则学习一个函数 ，将给定的潜在向量 再转换为观测值 。

公式（13）包含了两项。第一项是重构项，它度量了解码器从变分分布中重建输入的重构损失，这确保了所学习的分布对隐变量进行了有效的建模，我们可以从中重新生成出原始数据。第二项则衡量了学习到的变分分布与隐变量的先验分布（一般是标准正态分布）之间的相似程度。

VAE通常将编码器建模为具有对角协方差的多变量高斯分布，并选择标准多变量高斯分布作为先验分布：

然后，ELBO中的KL散度可以解析计算，并且可以使用蒙特卡罗估计来近似重建项：

其中， 是从 中进行采样得到的。

Hierarchical VAE

层次变分自动编码器（HVAE）是对VAE的推广，它将VAE扩展到了多层的隐变量。换句话说，隐变量本身被解释为由其他更高层次、更抽象的隐变量产生。

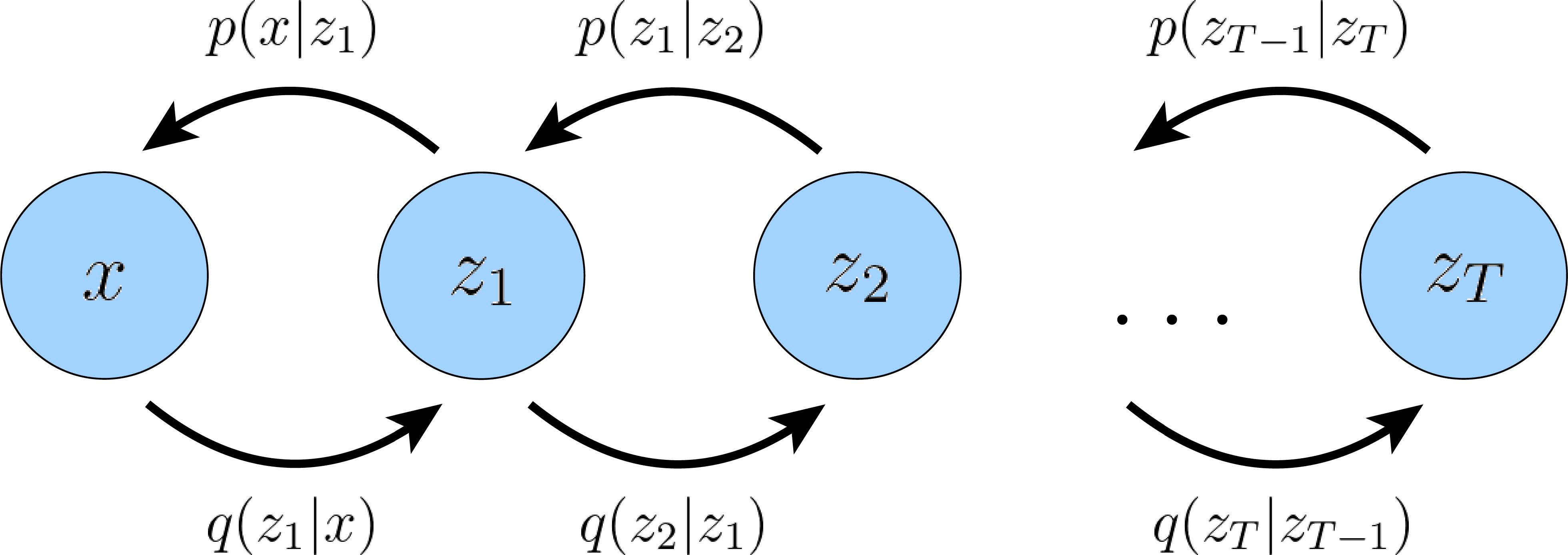
Hierarchical Variational Autoencoders

在 层的HVAE中，每个隐变量都建立在先前的隐变量条件之上。这里，我们专注于一种特殊情况，即马尔可夫HVAE（MHVAE）。MHVAE的生成过程是一个马尔可夫链。层次结构中的每一次向下转移都是马尔可夫的，所以每个隐变量 都仅以 为条件。

Variational Diffusion Models

有空再写，写不动啦，先鸽啦 (^_^)

Reference

[1]. Ho J, Jain A, Abbeel P. Denoising diffusion probabilistic models[J]. Advances in Neural Information Processing Systems, 2020, 33: 6840-6851.

[2]. Luo C. Understanding diffusion models: A unified perspective[J]. arXiv preprint arXiv:2208.11970, 2022.